Suatu derajat kebebasan  adalah kuadratik apabila the energi terkait dengan derajat kebebasan, dapat ditulis sebagai
adalah kuadratik apabila the energi terkait dengan derajat kebebasan, dapat ditulis sebagai
 ,
,
di mana  adalah kombinasi linear dari setiap derajat kebebasan kuadratik.
adalah kombinasi linear dari setiap derajat kebebasan kuadratik.
 adalah kombinasi linear dari setiap derajat kebebasan kuadratik.
adalah kombinasi linear dari setiap derajat kebebasan kuadratik.
contoh: jika 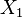 dan
dan  adalah dua derajat kebebasan, dan
adalah dua derajat kebebasan, dan  adalah energi asosiatif:
adalah energi asosiatif:
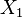 dan
dan  adalah dua derajat kebebasan, dan
adalah dua derajat kebebasan, dan  adalah energi asosiatif:
adalah energi asosiatif:- Jika
 , dengan dua derajat kebebasan yang tidak independen dan non-kuadratik.
, dengan dua derajat kebebasan yang tidak independen dan non-kuadratik. - Jika
 , dengan dua derajat kebebasan yang independen and non-quadratik.
, dengan dua derajat kebebasan yang independen and non-quadratik. - Jika
 , dengan dua derajat kebebasan yang tidak independen dan kuadratik.
, dengan dua derajat kebebasan yang tidak independen dan kuadratik. - Jika
 , dengan dua derajat kebebasan yang independen dan kuadratik.
, dengan dua derajat kebebasan yang independen dan kuadratik.
- Jika
Sebagai contoh, dalam Newtonian mechanics, dynamics suatu sistem dengan derajat kebebasan kuadratik diatur sehingga homogen persamaan differential linear dengankoefisien konstan.
Derajat Kebebasan Independen dan Kuadratik
 adalah derajat kebebasan kuadratik dan independen apabila energi assosiatif untuk keadaan mikro suatu sistem bisa dipresentasikan sebagai berikut:
adalah derajat kebebasan kuadratik dan independen apabila energi assosiatif untuk keadaan mikro suatu sistem bisa dipresentasikan sebagai berikut:Teorema Equipartisi
Pada batasan klasik mekanika statisti, pada equilibrium termodinamika, energi internal dari suatu sistem N derajat kebebasan independen dan kuadratik adalah:
Disini, mean energi assosiatif dengan derajat kebebasan adalah:
Apabila derajat kebebasan independen, energi internal dari sistem setara dengan jumlah rata-rata energi assosiatif dengan setiap derajat kebebasan, yang dapat ditunjukkan pada hasil.



