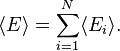Derajat kebebasan terdiri atas  suatu sistem yang independen jika energi assosiatif diatur bisa ditulis sebagai berikut:
suatu sistem yang independen jika energi assosiatif diatur bisa ditulis sebagai berikut:  di mana
di mana 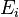 adalah fungsi dengan variabel tunggal
adalah fungsi dengan variabel tunggal  . example: jika
. example: jika 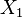 and
and  memiliki 2 derajat kebebasan, dan
memiliki 2 derajat kebebasan, dan  adalah energi assosiatif:
adalah energi assosiatif:
- Jika
 , dengan dua derajat kebebasan yang independen.
, dengan dua derajat kebebasan yang independen. - Jika
 , dengan dua derajat kebebasan yang tidak independen. Istilah yang melibatkan produk
, dengan dua derajat kebebasan yang tidak independen. Istilah yang melibatkan produk 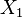 dan
dan  adalah istilah kopling, yang menggambarkan interaksi antara dua derajat kebebasan.
adalah istilah kopling, yang menggambarkan interaksi antara dua derajat kebebasan.
- Jika
Untuk i dari 1 to N, dengan iderajat kebebasan  didistribusikan berdasarkan distribusi Boltzmann. Probability fungsi kerapatan mengikuti:
didistribusikan berdasarkan distribusi Boltzmann. Probability fungsi kerapatan mengikuti:
 didistribusikan berdasarkan distribusi Boltzmann. Probability fungsi kerapatan mengikuti:
didistribusikan berdasarkan distribusi Boltzmann. Probability fungsi kerapatan mengikuti: ,
,
Pada bagian ini, seluruh artikel dengan tanda kurung  menunjukkan mean rata-rata jumlah.
menunjukkan mean rata-rata jumlah.
 menunjukkan mean rata-rata jumlah.
menunjukkan mean rata-rata jumlah.
Energi internal sistem merupakan jumlah dari rata-rata energi asosiatif untuk setiap derjat kebebasan:
Demonstrasi[sunting | sunting sumber]
Sebuah pertukaran energi sistem dalam bentuk panas dengan lingkungannya dan jumlah partikel dalam sistem tetap. Hal ini terkait dengan sistem dalam ansambel kanonik. Perhatikan bahwa dalam mekanika statistik, hasil yang ditunjukkan untuk sistem dalam ansambel tertentu tetap untuk sistem ini pada batas termodinamika dalam ansambel apapun. Dalam ansambel kanonik, kesetimbangan termodinamika, keadaan dari sistem didistribusikan di antara semua keadaan mikro berdasarkan distribusi Boltzmann. Jika  suhu sistem dan
suhu sistem dan  konstanta Boltzmann, maka probabilitas fungsi kerapatan yang terkait untuk setiap keadaan mikro adalah sebagai berikut:
konstanta Boltzmann, maka probabilitas fungsi kerapatan yang terkait untuk setiap keadaan mikro adalah sebagai berikut:
 suhu sistem dan
suhu sistem dan  konstanta Boltzmann, maka probabilitas fungsi kerapatan yang terkait untuk setiap keadaan mikro adalah sebagai berikut:
konstanta Boltzmann, maka probabilitas fungsi kerapatan yang terkait untuk setiap keadaan mikro adalah sebagai berikut: ,
,
Penyebut pada persamaan di atas memiliki peranan penting. Dalam hal ini, terbentuk produk bergantung pada derajat kebebasan tunggal.
Gangguan dari multidimensional probabilitas fungsi kepadatan menjadi fungsi produk dengan satu variabel sudah cukup untuk menunjukkan bahwa X_1 ![\ ldots X_N </ math> adalah [[statistik independen ]] satu sama lain.
Setiap fungsi <math>p_i](https://upload.wikimedia.org/math/2/3/b/23b827de812631a56285d2d0cae18553.png) adalah Konstanta Normalisasi, mengikuti bahwa
adalah Konstanta Normalisasi, mengikuti bahwa  adalah probabiliti fungsi kerapatan dari derajat kebebasan
adalah probabiliti fungsi kerapatan dari derajat kebebasan  , untuk i dari 1 sampai N.
, untuk i dari 1 sampai N.
![\ ldots X_N </ math> adalah [[statistik independen ]] satu sama lain.
Setiap fungsi <math>p_i](https://upload.wikimedia.org/math/2/3/b/23b827de812631a56285d2d0cae18553.png) adalah Konstanta Normalisasi, mengikuti bahwa
adalah Konstanta Normalisasi, mengikuti bahwa  adalah probabiliti fungsi kerapatan dari derajat kebebasan
adalah probabiliti fungsi kerapatan dari derajat kebebasan  , untuk i dari 1 sampai N.
, untuk i dari 1 sampai N.
Sehingga energi internal dari sistem merupakan energi rata-rata. Energi dari derajat kebebasan 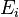 adalah fungsi dari variabel tunggal
adalah fungsi dari variabel tunggal  . Jika
. Jika  adalah statistik independent satu sama lain, maka energi
adalah statistik independent satu sama lain, maka energi  juga statistik independen satu sama lain. Total energi internal dari sistem bisa ditulis:
juga statistik independen satu sama lain. Total energi internal dari sistem bisa ditulis:
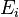 adalah fungsi dari variabel tunggal
adalah fungsi dari variabel tunggal  . Jika
. Jika  adalah statistik independent satu sama lain, maka energi
adalah statistik independent satu sama lain, maka energi  juga statistik independen satu sama lain. Total energi internal dari sistem bisa ditulis:
juga statistik independen satu sama lain. Total energi internal dari sistem bisa ditulis: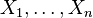 semua
semua